| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- rdbms nosql 차이
- 빅데이터 분석기사
- 모델 학습 및 예측
- 1일 1쿼리
- 네트워크 면접 답변
- 운영체제 면접 답변
- 빅분기 캐글놀이터
- 작업 2유형
- FLUTTER
- 빅분기 1유형
- 빅분기
- ?. ?? ! late
- 컴포지션과 집합
- SpringBoot와 .NET의 차이점
- 작업 1유형
- sqld 시험 정리
- SQL
- flutter 믹스인
- 빅분기 필기 pdf
- .NET 프레임워크 기초
- 주말에도 1일 1쿼리
- mysql mongo 성능 비교
- 빅분기 판다스 100제
- Mac OS .NET 개발환경
- .NET 게시판 프로젝트
- .NET Razor
- 오늘은 1일 2쿼리
- late 키워드
- MySQL
- 주말도 한다
- Today
- Total
subindev 님의 블로그
[실기] 빅데이터 분석기사 작업 3유형 본문
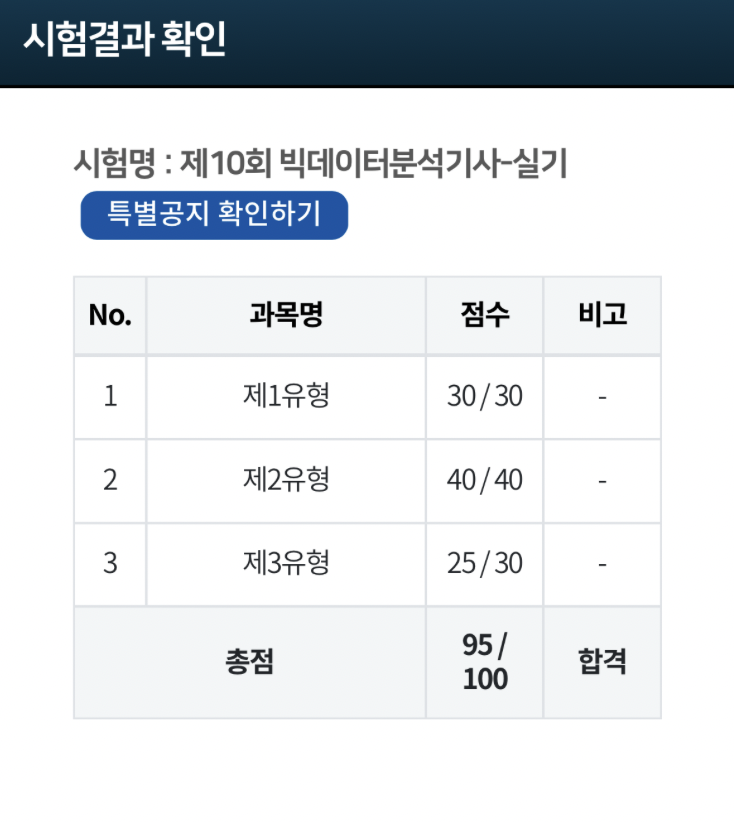
2025/06/21 시행한 시험 합격했어요!
일단 저는 컴퓨터 공학을 전공했고 데이터에 아예 무지한 상태는 아니였어요.
웹 개발 프로젝트 중 사용자 로그를 수집하여 분석하는 과제를 맡았었는데
그 때 빅데이터에 대한 관심이 생겨서 취득하게 되었습니다 : )
코테를 준비중이라 파이썬은 어느정도 익숙한 상태에서 시작하였고 실기 공부는 2주 정도 한 것 같습니다.
저는 2유형 제일 먼저 공부하시고 3유형 후 1유형을 하는 것을 추천 드리고 싶어요.
3유형은 아직 기출이 많이 없어 기출 위주로 핵심 내용만 익히고 갔는데 실수로 한문제 틀렸지만 다 풀 수 있겠더라구요!
또, 제 1유형은 python을 원래도 쓰실 수 있으시다면 크게 어려울 것 같지 않아요
help 와 dir을 이용하여서 기억 안나는 함수도 사용할 수 있기에 너무 걱정 안하셔도 될 거 같아요!
pandas 100제 문제 푸는 것이 python와 pandas를 처음 익히고 익숙해 지기에 너무 좋은 거 같아요
그치만 시험 대비로 생각한다면 약간 난이도가 있는거 같아서
다 완벽하게 풀지 못하여도 이런 함수가 있구나 정도만 익히시고 넘어가도 괜찮을 거 같습니다!
다들 화이팅입니다 :)
T-검정 / F-검정 / 로지스틱 회귀 / 카이제곱 / 다중회귀 / 상관계수 외워서 가기
Big Data Certification KR
퇴근후딴짓 의 빅데이터 분석기사 실기 (Python, R tutorial code) 커뮤니티
www.kaggle.com
T-검정
ttest_ind - 독립적인 두 그룹 (분산 같으면 equal_var = True)
ttest_rel - 동일한 대상 전, 후
ttest-1samp - 하나의 기준값과 비교
p-value < 0.05 - 유의미 - 대립가설 채택 - 귀무가설 기각
p-value ≥ 0.05 - 무의미 - 대립가설 기각 - 귀무가설 채택
귀무가설을 기준으로 alternative = 'two-sided' (다르다) / 'less' (적다) , 'greater' (많다)
import pandas as pd
from scipy.stats import ttest_ind, ttest_rel, ttest_1samp, chi2_contingency, pearsonr, f
import statsmodels.api as sm # 절편 추가
# ✅ 1. 독립표본 t-검정 (ttest_ind)
# 두 서로 다른 집단의 평균이 같은지 비교할 때 사용
# 예: 남자 그룹과 여자 그룹의 키 평균이 다른가?
g1 = df[df['그룹']=='A']['값']
g2 = df[df['그룹']=='B']['값']
from scipy.stats import levene
result = levene(group1, group2)
print(result) # p_value > 0.05 - 무의미 - 대립가설(차이 있다)기각 - 분산 같다
t_stat, p = ttest_ind(g1, g2, equal_var=True, alternative = 'two-sided')
print(round(t_stat, 3), round(p, 3))
# p-value - 0.05보다 작으면 통계적으로 유의미하다 평균 차이가 있다 - 귀무가설 기각
# result = ttest_ind(g1, g2) 해서 print 해도 찾을 수 있음
# ✅ 2. 대응표본 t-검정 (ttest_rel)
# 동일한 대상의 전/후 값을 비교할 때 사용
# 예: 다이어트 전/후 몸무게 비교
t_stat, p = ttest_rel(df['전'], df['후'])
print(round(t_stat, 3), round(p, 3))
# ✅ 3. 단일표본 t-검정 (ttest_1samp)
# 한 집단의 평균이 기준값과 다른지 검정
# 예: 학생 평균 수학 점수가 70점과 차이가 있는가? - 귀무가설
t_stat, p = ttest_1samp(df['값'], popmean=70, alternative = 'two-sided')
print(round(t_stat, 3), round(p, 3))
로지스틱 회귀 (logit)
종속변수가 0 또는 1일 때 사용 (분류 문제)
# ✅ 4. 로지스틱 회귀 (logit)
import pandas as pd
from statsmodels.formula.api import logit
df = pd.read_csv("/kaggle/input/bigdatacertificationkr/Titanic.csv")
# 절편 상관 안써도 됨, 범주형 데이터 신경 안써도 됨
formula = "Survived ~ C(Pclass) + Gender + SibSp + Parch"
model = logit(formula, data=df).fit()
print(model.summary()) # 이걸 추천
print(model.params) # -0.049847
# parch 변수나 Pseudo R-Square 등등 찾을 수 있음
from statsmodels.api as sm
X = sm.add_constant(X)
model = sm.Logit(y,X).fit()
results = model.fit()
print(results.sammary())
다중 선형 회귀 (OLS)
# ✅ 6. 다중 선형 회귀 (OLS)
# 여러 수치형 변수로 결과값(수치형)을 예측할 때 사용
# 예: 수입을 나이, 근속연수, 가족 수로 예측
# 필요한 라이브러리 임포트
from statsmodels.formula.api import ols, logit
from statsmodels.formula.api import ols, logit
# 모든 변수를 사용하여 ols 모델을 적합하고, 회귀계수 중 가장 큰 값은?
# coef(계수) 중 부호 제외 제일 큰 값
model_full = ols('y ~ x1 + x2 + x3 + x4', data = data).fit()
print(model_full.summary()) # 1. x1
# 유의미하지 않은 변수를 제수를 제거한 뒤 모델을 다시 적합하고, 회귀 계수 중 가장 작은 변수명은?
# P > |t| - 0.05를 넘는다면 무의미
model_2 = ols('y ~ x1 + x2 + x3', data = data).fit()
print(model_2.summary())
# 훈련데이터의 예측값과 실제값의 피어슨 상관계수를 구하시오
import statsmodels.api as sm
test = df[df['id']>140]
X = df[df['id']<=140]
y = X['tenure']
X = X.drop(['tenure'], axis=1)
X_const = sm.add_constant(X)
model = sm.OLS(y,X_const).fit()
pred = model.predict(X_const)
pred.corr(y) # spearman , kendall
pred.corr(y, method = 'pearson')

카이제곱 검정
# ✅ 5. 카이제곱 검정 (chi2_contingency)
# 두 범주형 변수 간 관련성(독립성) 있는지 확인
# 예: 성별과 상품 구매 여부가 관련이 있는가?
# 카이 제곱은 크로스 테이블 생성
from scipy.stats import chi2_contingency
table = pd.crosstab(df['gender'],df['survived'])
print(chi2_contingency(table))
# chi2 , p-value, ddof , expected
F-검정
# ✅ 8. F검정 (f.cdf)
# 두 집단의 분산(흩어진 정도)에 차이가 있는지 검정
# 예: 남자와 여자의 수입 분산이 다른가?
g1 = df[df['성별'] == '남']['수입']
g2 = df[df['성별'] == '여']['수입']
var1 = g1.var() # var1 = np.var(g1, ddof=1)
var2 = g2.var()
f_stat = max(var1, var2) / min(var1, var2)
df1 = len(g1) - 1 # 분자 자유도
df2 = len(g2) - 1 # 분모 자유도
# 합동 분산 추정
(df1 * var1 )+ (df2 * var2) / df1 + df2
print("F 통계량:", round(f_stat, 3))
p_val = 1 - f.cdf(f_stat, dfn=df1, dfd=df2)
print("p값:", round(p_val, 3))
피어슨 상관계수 / 스피어만 상관계수
# 훈련데이터의 예측값과 실제값의 피어슨 상관계수를 구하시오
import statsmodels.api as sm
test = df[df['id']>140]
X = df[df['id']<=140]
y = X['tenure']
X = X.drop(['tenure'], axis=1)
X_const = sm.add_constant(X)
model = sm.OLS(y,X_const).fit()
pred = model.predict(X_const)
pred.corr(y) # spearman , kendall
pred.corr(y, method = 'pearson')
# ✅ 7. 상관계수 분석 (pearsonr)
# 두 수치형 변수 간 선형적 관계의 강도 확인 (상관관계)
# 예: 공부시간과 점수 간의 관계
corr, p = pearsonr(df['공부시간'], df['점수'])
print(round(corr, 3), round(p, 3))
포아송 - poisson .pdf .cmf(1, lambda_)
from scipy.stats import poisson
lambda_ = 3
print(poisson.pmf(5, lambda_)) # 몇번 발생활 확률 pmf
print(poisson.cdf(1, lambda_)) # 몇번 이하로 발생할 확률 cdf
import scipy.stats import poisson
lambda_ = 3
print(poisson.pmf(5, lambda_))
print(poisson.cdf(3, lambda))'데이터 관련 > 빅데이터 분석기사' 카테고리의 다른 글
| [실기] 빅데이터 분석기사 작업 2유형(6문제) (2) | 2025.07.09 |
|---|---|
| [실기] 빅데이터 분석기사 작업 1유형(35문제) (1) | 2025.06.24 |
| [실기] 빅데이터 분석기사 python - pandas 100제 문제 (1) | 2025.06.24 |
| [필기] 빅데이터 분석기사 필기 요약정리(pdf 파일 첨부) (1) | 2025.06.14 |




